문제 보기
https://www.acmicpc.net/problem/1004
1004번: 어린 왕자
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 첫째 줄에 출발점 (x1, y1)과 도착점 (x2, y2)이 주어진다. 두 번째 줄에는 행성계의 개수 n이 주
www.acmicpc.net
문제
어린 왕자는 소혹성 B-664에서 자신이 사랑하는 한 송이 장미를 위해 살아간다. 어느 날 장미가 위험에 빠지게 된 것을 알게 된 어린 왕자는, 장미를 구하기 위해 은하수를 따라 긴 여행을 하기 시작했다. 하지만 어린 왕자의 우주선은 그렇게 좋지 않아서 행성계 간의 이동을 최대한 피해서 여행해야 한다. 아래의 그림은 어린 왕자가 펼쳐본 은하수 지도의 일부이다.

빨간 실선은 어린 왕자가 출발점에서 도착점까지 도달하는데 있어서 필요한 행성계 진입/이탈 횟수를 최소화하는 경로이며, 원은 행성계의 경계를 의미한다. 이러한 경로는 여러 개 존재할 수 있지만 적어도 3번의 행성계 진입/이탈이 필요하다는 것을 알 수 있다.
위와 같은 은하수 지도, 출발점, 도착점이 주어졌을 때 어린 왕자에게 필요한 최소의 행성계 진입/이탈 횟수를 구하는 프로그램을 작성해 보자. 행성계의 경계가 맞닿거나 서로 교차하는 경우는 없다. 또한, 출발점이나 도착점이 행성계 경계에 걸쳐진 경우 역시 입력으로 주어지지 않는다.
입력
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 첫째 줄에 출발점 (x1, y1)과 도착점 (x2, y2)이 주어진다. 두 번째 줄에는 행성계의 개수 n이 주어지며, 세 번째 줄부터 n줄에 걸쳐 행성계의 중점과 반지름 (cx, cy, r)이 주어진다.
출력
각 테스트 케이스에 대해 어린 왕자가 거쳐야 할 최소의 행성계 진입/이탈 횟수를 출력한다.
제한
- -1000 ≤ x1, y1, x2, y2, cx, cy ≤ 1000
- 1 ≤ r ≤ 1000
- 1 ≤ n ≤ 50
- 좌표와 반지름은 모두 정수
그림의 동그라미와 곡선을 보자마자 첫 인상은 좋지는 않았으나
문제를 읽다보면 푸는 방법을 쉽게 알아낼 수 있다.
저번 1002번 터렛 문제와 비슷하게
원의 방정식을 이용한 문제이다.
https://mountain-noroo.tistory.com/12
[백준][C#] 1002 터렛 - 실버3
문제 보기 https://www.acmicpc.net/problem/1002 1002번: 터렛 각 테스트 케이스마다 류재명이 있을 수 있는 위치의 수를 출력한다. 만약 류재명이 있을 수 있는 위치의 개수가 무한대일 경우에는 -1을 출력
mountain-noroo.tistory.com
물론 터렛보다 훨씬 간단하다.
6가지 경우의 수를 따져보아야 했던 것과 달리,
출발 좌표와 도착 좌표가 원 안에 있냐, 없냐만을 판별하면 되기 때문이다.
행성계(원)에 진입한 횟수 + 이탈한 횟수를 출력하는 문제이기에
진입+이탈이 어떤 상황에서 이루어지는지 살펴보아야 한다.
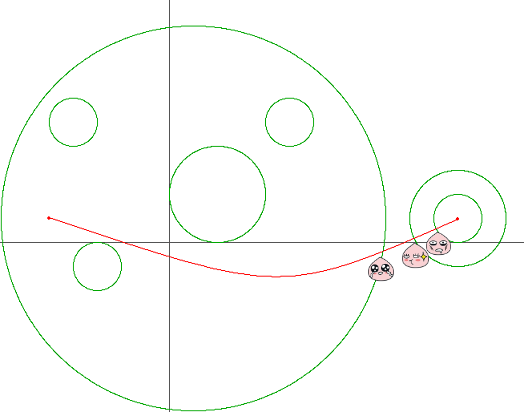
문제의 그림을 살펴보면 이탈이 1번, 진입이 2번 이루어졌다.
더 자세히 살펴보면
이탈은 시작점의 좌표를 내부에 가진 원에서 나올 때 이루어졌고,
진입은 도착점의 좌표를 내부에 가진 원으로 들어갈 때 이루어졌다.
즉
내부에 시작점의 좌표를 가지고 있는 원의 수
내부에 도착점의 좌표를 가지고 있는 원의 수를 더해주면 되는 것이다.
(원이 교차하거나 맞닿는 경우는 없기 때문)
그러나 하나 더 짚고 넘어가야 하는 부분이 있다.

만약 이 그림의 외부에도 이렇게 원이 있었다면?
진입, 이탈에는 전혀 영향을 주지 않지만 시작점, 도착점 모두 이 원에 포함되기 때문에
방금과 같은 식을 사용한다면 count가 2나 늘어나버리고 말 것이다.
어차피 같은 원 안에 있는 것이라면
굳이 나갈 필요도, 들어갈 필요도 없다.
애초에 카운팅하지 않아도 되는 일이다.
for (int i = 0; i < n; i++)
{
// 원의 반지름이 시작(도착)좌표에서 원의 중점까지의 길이보다 큰가?
// 원의 내부에 좌표가 존재하냐를 판별 후, bool 배열에 넣어주었음.
if (planets[i].r > Math.Sqrt(Math.Pow(startX - planets[i].x, 2) + (Math.Pow(startY - planets[i].y, 2))))
{
isStartPoinInPlanets[i] = true;
}
if (planets[i].r > Math.Sqrt(Math.Pow(endX - planets[i].x, 2) + (Math.Pow(endY - planets[i].y, 2))))
{
isEndPoinInPlanets[i] = true;
}
}
int count = 0;
for (int i = 0; i < n; i++)
{
// 시작점이 내부에 있고 도착점은 외부에 있는 경우
// or
// 도착점이 내부에 있고 시작점이 외부에 있는 경우
if (!isStartPoinInPlanets[i] && isEndPoinInPlanets[i] || isStartPoinInPlanets[i] && !isEndPoinInPlanets[i])
{
count++;
}
}
코드 보기
static void Main(string[] args)
{
using var reader = new System.IO.StreamReader(Console.OpenStandardInput());
using var print = new System.IO.StreamWriter(Console.OpenStandardOutput());
string input = reader.ReadLine();
int t = int.Parse(input);
for(int j = 0; j < t; j++)
{
input = reader.ReadLine();
int startX = int.Parse(input.Split()[0]);
int startY = int.Parse(input.Split()[1]);
int endX = int.Parse(input.Split()[2]);
int endY = int.Parse(input.Split()[3]);
input = reader.ReadLine();
int n = int.Parse(input);
(int x, int y, int r)[] planets = new (int, int, int)[n];
for (int i = 0; i < n; i++)
{
input = reader.ReadLine();
planets[i].x = int.Parse(input.Split()[0]);
planets[i].y = int.Parse(input.Split()[1]);
planets[i].r = int.Parse(input.Split()[2]);
}
bool[] isStartPoinInPlanets = new bool[n];
bool[] isEndPoinInPlanets = new bool[n];
for (int i = 0; i < n; i++)
{
if (planets[i].r > Math.Sqrt(Math.Pow(startX - planets[i].x, 2) + (Math.Pow(startY - planets[i].y, 2))))
{
isStartPoinInPlanets[i] = true;
}
if (planets[i].r > Math.Sqrt(Math.Pow(endX - planets[i].x, 2) + (Math.Pow(endY - planets[i].y, 2))))
{
isEndPoinInPlanets[i] = true;
}
}
int count = 0;
for (int i = 0; i < n; i++)
{
if (!isStartPoinInPlanets[i] && isEndPoinInPlanets[i] || isStartPoinInPlanets[i] && !isEndPoinInPlanets[i])
{
count++;
}
}
print.WriteLine(count);
}'ProblemSolve' 카테고리의 다른 글
| [백준][C#] 15649 N과 M (1) - 실버3 (0) | 2023.06.17 |
|---|---|
| [백준][C#] 2407 조합 - 실버3 (0) | 2023.06.16 |
| [백준][C#] 9375 패션왕 신해빈 - 실버3 (0) | 2023.06.14 |
| [백준][C#] 1002 터렛 - 실버3 (0) | 2023.06.14 |
| [백준][C#] 9095 1, 2, 3 더하기 - 실버3 (1) | 2023.06.13 |