99클럽 코테 스터디 22일차 TIL (챌린저): [프로그래머스][Java] 산 모양 타일링 - level3

 

문제 보기

https://school.programmers.co.kr/learn/courses/30/lessons/258705

프로그래머스

 

 

풀이

문제를 읽고 dp로 풀어야겠다는 감이 왔다.

더 적은 삼각형으로 이루어진 도형을 가지고 다음을 유추해 볼 수 있기 때문이다.

n-1의 도형에서 새로 놓을 수 있는 마름모는 정해져 있기 때문에 식을 잘 세우면 되지 않을까?

위의 경우는 새로운 마름모를 두지 않았을 때,
왼쪽에 치우친 마름모를 두었을 때,
똑바로 선 마름모를 두었을 때,
오른쪽에 치우친 마름모를 두었을 때로 예시를 분류해 본 것이다.

 

그러나 아직 식을 세우기엔 애매한 점이 있었다.

n-1에 대한 식으로만 세우기엔 왼쪽으로 기울어진 삼각형은 어떻게 계산해야 할 지였다.

 

그래서 n이 아닌 삼각형 하나에 대한 dp를 세우기로 했다.

위에 붙은 삼각형은 역삼각형(홀수) 경우의 수를 셀 때 같이 고려해 볼 것이다.

int[] dp = new int[n * 2 + 1];
dp[0] = 1;
if(tops[0] == 0) {
  dp[1] = 2;
  dp[2] = 3;
} else {
  dp[1] = 3;
  dp[2] = 4;
}

시작 전에 우선 0, 1, 2의 경우의 수는 직접 채워 넣었다.

 

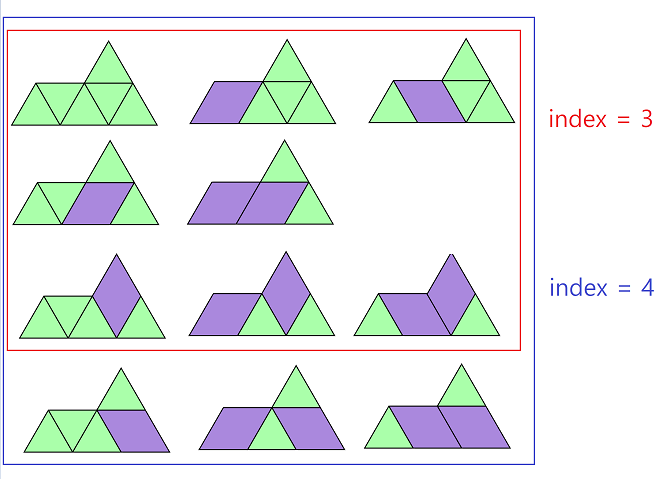
그리고 방금 봤던 그림을 index 3일 경우, 4일 경우로 나눠 봤다.

더 깊숙히 들어가 보자.

 

짝수

index 4는

index 2인 경우에 오른쪽으로 치우친 마름모를 넣은 경우

+ index 3인 경우 전체이다.

dp[i] = dp[i - 1] + dp[i - 2]

 

홀수

index 3는

index 2인 경우에 똑바로 선 마름모를 넣은 경우

+ index 2인 경우에 아무 마름모도 넣지 않은 경우

+ index 1인 경우에 왼쪽으로 치우친 마름모를 넣은 경우이다.

dp[i] = dp[i - 1] + dp[i - 1] + dp[i - 2];

물론 여기서 tops가 0인 경우에는 똑바로 선 마름모를 넣은 경우가 없어지므로

dp[i] = dp[i - 1] + dp[i - 2];

위와 같다.

 

이를 정리해 보자.

for(int i = 1, j = 3; i < n; i++, j+=2) {
  if(tops[i] == 0) {
    dp[j] = (dp[j - 1] + dp[j - 2]) % 10007;
  } else {
    dp[j] = (dp[j - 1] + dp[j - 1] + dp[j - 2]) % 10007;
  }
  dp[j + 1] = (dp[j] + dp[j - 1]) % 10007;
}

 

 

전체 코드

class Solution {
  public int solution(int n, int[] tops) {
    int[] dp = new int[n * 2 + 1];
    dp[0] = 1;
    if(tops[0] == 0) {
      dp[1] = 2;
      dp[2] = 3;
    } else {
      dp[1] = 3;
      dp[2] = 4;
    }

    for(int i = 1, j = 3; i < n; i++, j+=2) {
      if(tops[i] == 0) {
        dp[j] = (dp[j - 1] + dp[j - 2]) % 10007;
      } else {
        dp[j] = (dp[j - 1] + dp[j - 1] + dp[j - 2]) % 10007;
      }
      dp[j + 1] = (dp[j] + dp[j - 1]) % 10007;
    }

    return dp[n * 2];
  }
}

 

 

GitHub 링크

https://github.com/MetroDefro/CodingTest_AutoSave/tree/main/%ED%94%84%EB%A1%9C%EA%B7%B8%EB%9E%98%EB%A8%B8%EC%8A%A4/3/258705.%E2%80%85%EC%82%B0%E2%80%85%EB%AA%A8%EC%96%91%E2%80%85%ED%83%80%EC%9D%BC%EB%A7%81

CodingTest_AutoSave/프로그래머스/3/258705. 산 모양 타일링 at main · MetroDefro/CodingTest_AutoSave